さて、こちらに２種類のかたつむりのイラストがあります。よく見ると、うずまきの描き方が違います。　あなたはＡとＢ、どちらの殻のかたつむりが好みですか？

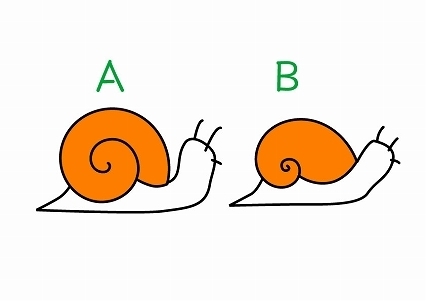
　実は、これらはそれぞれ異なる数学的規則に基づいたうずまき（螺旋形）を描いています。
　Ａはアルキメデスの螺旋呼ばれる形。Ｂは対数螺旋（等角螺旋、ベルヌーイの螺旋とも言います）と呼ばれます。　Ａを極座標の方程式で表すと、次のようになります。

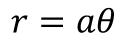
　…っていうか、そもそも極座標とは、なんでしょう。
　まずは、ふつうの座標について説明します。x軸とy軸があって、(x,y）で１点を表すことのできる座標です。直交座標とも言います。　点Ｐが（1，1）とあれば、xが1で、yが1の点なので、点Ｐの位置はこんな風に示すことができます。

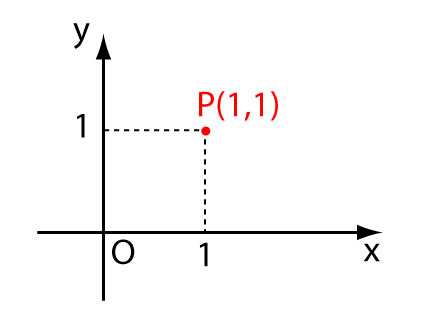
　一方、極座標は、x軸とy軸の代わりに、中心Oからの距離rと、回転角θで、点（r,θ）を表す座標のことです。　点Qが（√2, 45°）とあれば、中心Oから45°の角度で√2だけ進んだ点なので、こんな位置になります。

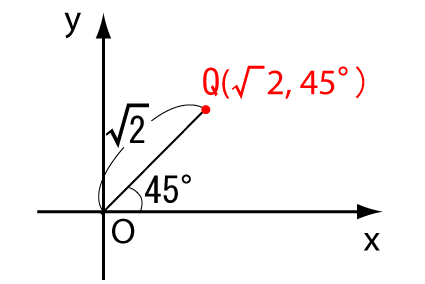
　おおざっぱに言えば、ふつうの直交座標が折れ線グラフ、極座標はレーダーチャート、という感じですね。

　さて、直交座標で、y=axのグラフを書くと、右肩上がりの直線が引けます。　　同じように、極座標で、r=aθのグラフを書くと、さっきのアルキメデスのらせんになるのです。　θ=1°のときr=1、θ=2°のときr=2というように、θの値を少しずつ増やして描いていくと、結果的に幅が一定のうずまきを描くことになります。（ちなみに、a>0なら左巻き。a<0なら右巻きになります）
　それが、冒頭のＡのかたつむり。マンガ的なかたつむりは、こんな螺旋が多いですね。　もう一度見てみましょう。

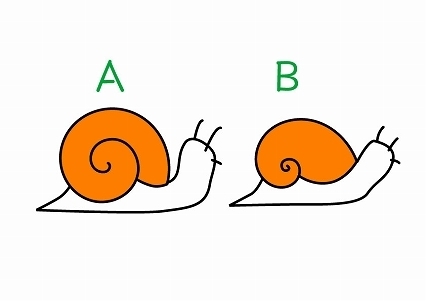
　さて、Ａのかたつむりに比べ、Ｂの方がリアリティがありませんか。　そして、なにより、かわいく見えませんか？　←主観
　Ｂのかたつむりの殻は、極座標の方程式で、次のように表すことができます。

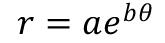
　こちらは、b<0なら右巻き。b>0なら左巻きになります。（eは自然対数の底を表す定数で、e=2.7182818…という無理数で、特別な性質があるのですが、ここでは省略します。）　　実際に、かたつむりを含む巻き貝のなかま、オウムガイやアンモナイトのなかまなどの殻は、すべてこの対数螺旋に当てはまります。　中心からの距離が角度に対して指数関数的に増大していくので、幅がだんだん広がっていくうずまきになります。　幅の広がり方はbの値によって変わります。イラストは大きめにしていますが、もっとアルキメデスの螺旋に似せることもできます。　自然界には、こうした対数螺旋が多く見られます。実は二枚貝も厳密には螺旋形で、このbを大きな値にすると、二枚貝っぽくなります。　そしてさらに、たとえば台風のうずまき、銀河系のうずまきも、対数螺旋を描いています。

　螺旋が描ける方程式は、ほかにもいくつかあります。　興味がわいた方は調べてみてくださいね。
　数学ってこんな風に、物の形と関連しているのがおもしろいなぁと思います。　かたつむりと銀河系が同じ法則でつながっているなんて、不思議ですよね。
　これに限らず、自然界の物の形がいろいろな規則に当てはまっていることに気づくと、とてもおもしろいです。　一方で、そんな規則からちょっとずつズレているのを見つけるのもまた、自然界の面白さだと私は思います。
　ちなみに、「パスカルの蝸牛形」というのもあるそうです。

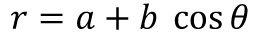
　「蝸牛」とはずばり、かたつむりのこと。ただし、残念ながらこれ、うずまきではないのです。　興味のある方は「パスカルの蝸牛形」でググってみると出てきますよー。